Đại số Boolean là một phương pháp toán học đặc biệt để biểu diễn mối quan hệ (logic) giữa các biến. Khung nhị phân của nó đơn giản hóa các phép toán phức tạp thành logic đúng (1)/sai (0), khiến nó trở nên không thể thiếu đối với các kỹ sư và lập trình viên.

• Đại số Boolean sử dụng các toán tử như AND, OR và NOT để mô hình hóa các quyết định logic, tạo thành cơ sở của mọi hệ thống số.
• Nó rất cần thiết để tạo ra các cổng logic, mạch tổ hợp và bộ nhớ hiệu quả trong phần cứng.
• Các kỹ thuật như bản đồ Karnaugh và định luật Boolean làm giảm độ phức tạp của mạch, tiết kiệm chi phí và điện năng.
• Nó mang theo logic có điều kiện, thuật toán tìm kiếm và truy vấn cơ sở dữ liệu trong phát triển phần mềm.

Các toán tử Boolean cơ bản và cổng logic

Toán tử Boolean được sử dụng để thực hiện các phép toán logic trên các giá trị Boolean. Cổng logic là các thiết bị vật lý hoặc mạch được sử dụng để thực hiện các phép toán Boolean cơ bản. Mỗi cổng logic thực hiện một phép toán cụ thể dựa trên logic Boolean.

1. Toán tử Boolean

• AND ( ∧ ): Toán tử AND trả về True (1) chỉ khi cả hai toán hạng đều là True (1).
• HOẶC ( ∨ ): Toán tử HOẶC trả về True (1) nếu ít nhất một trong các toán hạng là True (1).
• NOT ( ¬ ): Toán tử NOT đảo ngược giá trị của toán hạng. Nó trả về True (1) nếu toán hạng là False (0) và False (0) nếu toán hạng là True (1).
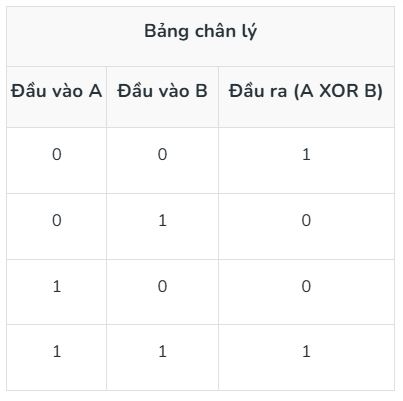
• XOR (OR loại trừ) (⊕): Toán tử XOR trả về True (1) nếu các toán hạng khác nhau và False (0) nếu chúng giống nhau.

2. Cổng logic

1. Cổng AND:  Cổng AND thực hiện phép toán AND. Nó 1 chỉ xuất ra nếu cả hai đầu vào đều là

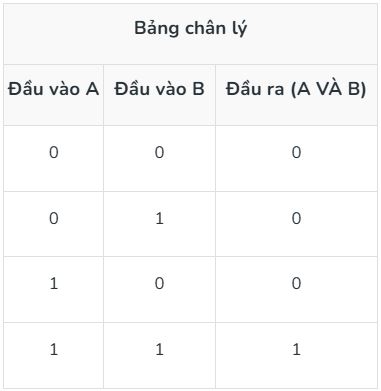
2. Cổng OR:  Cổng OR thực hiện phép toán OR. Nó sẽ xuất ra 1 nếu có ít nhất một đầu vào là

3. Cổng NOT:  Cổng NOT thực hiện phép toán NOT. Nó đảo ngược đầu vào, đưa ra kết quả 1 nếu đầu vào là 0 0 và 0 nếu đầu vào là 1.

4. Cổng NAND:  Cổng NAND là cổng ngược của cổng AND. Nó 0 chỉ xuất ra nếu cả hai đầu vào đều bằng 1; nếu không, nó xuất ra 1.

5. Cổng NOR:  Cổng NOR là cổng đảo ngược của cổng OR. Nó cho ra giá trị 0 nếu có ít nhất một đầu vào là 1; ngược lại, nó cho ra giá trị 1.

6. Cổng XOR: Cổng XOR thực hiện phép toán XOR. Nó sẽ đưa ra kết quả 1 nếu các đầu vào khác nhau và 0 nếu chúng giống nhau.

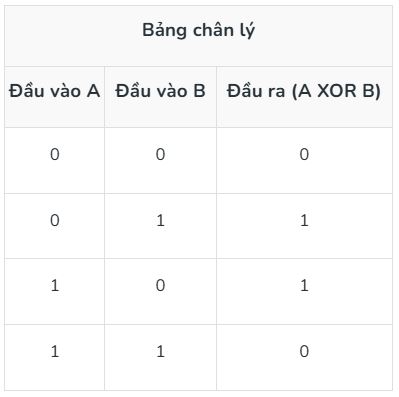
7. Cổng XNOR:  Cổng XNOR là phép toán ngược của phép toán XOR. Nó cho biết 1 đầu vào có giống nhau 0 hay khác nhau.

Các định luật và định lý cơ bản của đại số Boolean

Các định luật và định lý cơ bản của đại số Boolean giúp đơn giản hóa các biểu thức logic và hỗ trợ thiết kế mạch số. Một số định luật và định lý cốt lõi trong đại số Boolean là:

1. Luật giao hoán

Luật Giao hoán phát biểu rằng thứ tự kết hợp hai biến bằng toán tử AND hoặc OR không ảnh hưởng đến kết quả. Luật này cho phép chúng ta sắp xếp lại các số hạng mà không làm thay đổi kết quả đầu ra.

• Luật giao hoán cho AND :

A⋅B = B⋅A

Ví dụ:

1⋅0 = 0⋅1 = 0

• Luật giao hoán cho OR :

A + B = B + A

Ví dụ:

1 + 0 = 0 + 1 = 1

2. Luật kết hợp

Luật Kết hợp phát biểu rằng khi kết hợp ba hoặc nhiều biến bằng toán tử AND hoặc OR, việc nhóm các biến không ảnh hưởng đến kết quả. Luật này cho phép chúng ta nhóm lại các số hạng mà không làm thay đổi kết quả đầu ra.

• Luật kết hợp cho AND :

A⋅(B⋅C) = (A⋅B)⋅C

Ví dụ:

1⋅(0⋅1) = (1⋅0)⋅1 = 0

• Luật liên kết cho OR :

A + (B + C) = (A + B) + C

Ví dụ:

1 + (0 + 1) = (1 + 0) + 1 = 1

3. Luật phân phối

Luật phân phối mô tả cách các phép toán AND và OR phân phối cho nhau. Nó tương tự như cách phép nhân phân phối cho phép cộng trong số học. Luật này cho phép phân tích các biểu thức Boolean thành nhân tử, tương tự như phân tích các biểu thức đại số.

• Luật phân phối cho AND trên OR :

A⋅(B + C) = (A⋅B) + (A⋅C)

Ví dụ:

1⋅(0 + 1) = (1⋅0) + (1⋅1) = 0 + 1 = 1

• Luật phân phối cho OR trên AND :

A + (B⋅C) = (A + B)⋅(A + C)

Ví dụ:

1 + (0⋅1) = (1 + 0)⋅(1 + 1) = 1⋅1 = 1

4. Luật nhận dạng

Định luật Đồng nhất quy định rằng bất kỳ biến nào được AND với 1 hoặc OR với 0 sẽ cho kết quả là chính biến ban đầu. Định luật này cho thấy các phần tử đồng nhất cho phép toán AND và OR lần lượt là 1 và 0.

• Luật đồng nhất cho AND :

A⋅1 = A

Ví dụ:

1⋅1 = 1

• Luật nhận dạng cho OR :

A + 0 = A

Ví dụ:

1 + 0 = 1

5. Luật bổ sung

Định luật bù liên quan đến phép phủ định của một biến và cho kết quả khi một biến được kết hợp với phần bù của nó (đối lập). Định luật này cho thấy một biến được AND với phần bù của nó sẽ luôn bằng 0 và một biến được OR với phần bù của nó sẽ luôn bằng 1.

• Luật bù cho AND :

A⋅A' = 0

Ví dụ:

1⋅1' = 1⋅0 = 0

• Luật bổ sung cho OR :

A+A' = 1

Ví dụ:

1 + 1' = 1 + 0 = 1

6. Luật đảo ngược

Luật nghịch đảo là một nguyên lý độc đáo trong đại số Boolean, phát biểu rằng phần bù của phần bù của bất kỳ biến nào đều bằng chính biến đó.

(A') = A

Ví dụ:

(1')' = (0)' = 1

7. Định lý De Morgan

Định lý De Morgan cung cấp một cách để đơn giản hóa các biểu thức có phủ định và rất hữu ích trong thiết kế mạch kỹ thuật số.

Định lý đầu tiên của De Morgan : Phủ định của phép toán AND bằng phép toán OR của phủ định của các toán hạng.

(A⋅B)' = A' + B'

Ví dụ:

Biểu thức: (1⋅0)'

Đơn giản hóa: 1' + 0' = 0 + 1 = 1

Định lý thứ hai của De Morgan : Phủ định của phép toán OR bằng phép toán AND của phủ định của các toán hạng.

(A+B)' = A'⋅B'

Ví dụ:

Biểu thức: (1 + 0)'

Rút gọn: 1'⋅0' = 0⋅1 = 0

Ví dụ về Đại số Boolean

Chúng ta hãy giải một biểu thức Boolean:

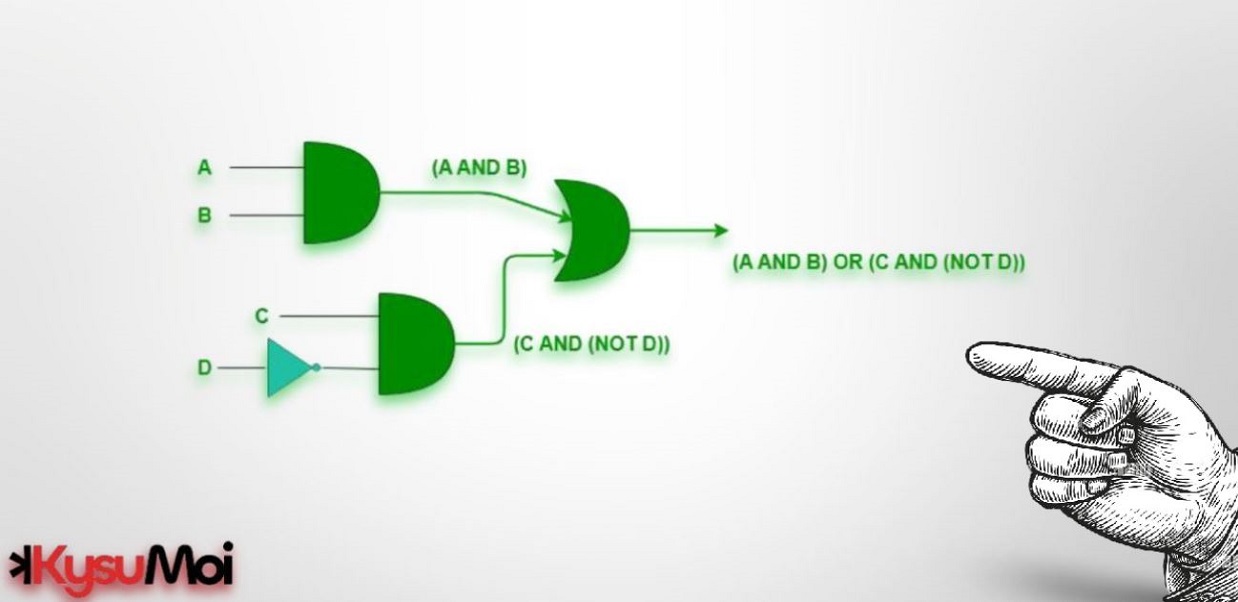
(A ∧ B) ∨ (C ∧ (¬D)) 

Cho A = B = 1, C = 0, D = 0.

Giải pháp: Hãy thay thế biểu thức bằng các giá trị cho sẵn từng phần một.

• (A ∧ B) = (1  ∧ 1) = 1
• (C  ∧ (¬D)) = (0 ∧ (¬0)) = (0 ∧ 1) = 0
• (A ∧ B) ∨ (C  ∧ (¬D)) = (1 ∨ 0) = 1

Vì vậy, câu trả lời cuối cùng cho biểu thức Boolean đã cho là 1.

Chúng ta hãy hiểu nó bằng cách sử dụng bảng chân lý, giả sử:

Y= (A ∧ B) ∨ (C ∧ (¬D)) 

Sơ đồ mạch logic của ví dụ trên :

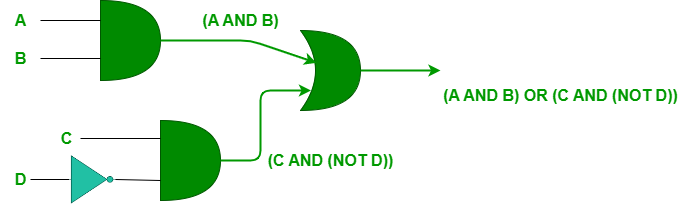
Sơ đồ mạch logic cho ví dụ đã cho

Ứng dụng của Đại số Boolean

1. Thiết kế mạch số : Đại số Boolean đơn giản hóa việc thiết kế các mạch tổ hợp và tuần tự như bộ cộng, bộ ghép kênh, flip-flop và thanh ghi, tối ưu hóa hiệu suất và cách sử dụng cổng.
2. Đơn giản hóa biểu thức logic : Đại số Boolean làm giảm các biểu thức logic phức tạp, giảm thiểu số lượng cổng cần thiết và cải thiện hiệu suất mạch cũng như mức tiêu thụ điện năng.
3. Thiết kế mạch số học : Được sử dụng để thiết kế các bộ cộng, trừ, nhân và chia nhị phân, cần thiết cho các phép tính số học nhị phân trong hệ thống số.
4. Thiết kế các thành phần bộ nhớ : Đại số Boolean giúp thiết kế các đơn vị bộ nhớ như flip-flop, chốt và thanh ghi, giúp lưu trữ dữ liệu và quản lý quá trình chuyển đổi trạng thái trong các mạch tuần tự.
5. Phát hiện và sửa lỗi : Được sử dụng trong các kỹ thuật phát hiện lỗi (ví dụ: kiểm tra chẵn lẻ) và sửa lỗi (ví dụ: mã Hamming) để đảm bảo tính toàn vẹn của dữ liệu trong hệ thống truyền thông.
6. Hệ thống điều khiển và bộ điều khiển logic : Đại số Boolean đóng vai trò quan trọng trong việc thiết kế logic điều khiển cho các hệ thống như máy trạng thái hữu hạn (FSM) và bộ điều khiển logic lập trình (PLC), giúp quản lý các quy trình tự động.
7. Tối ưu hóa thiết kế mạch : Giúp giảm độ phức tạp của mạch kỹ thuật số, giảm số lượng cổng, giảm thiểu không gian và cải thiện hiệu suất năng lượng trong IC, FPGA và ASIC.
8. Hệ thống mật mã và bảo mật : Đại số Boolean được ứng dụng trong thiết kế mạch mã hóa và giải mã, hỗ trợ truyền dữ liệu an toàn và xác thực trong các hệ thống bảo mật kỹ thuật số.
9. Xử lý tín hiệu số (DSP) : Được sử dụng để xử lý tín hiệu số cho các tác vụ như lọc, mã hóa và chuyển đổi âm thanh, video và các tín hiệu khác sang định dạng kỹ thuật số.