Trong thế giới điện tử và xử lý số liệu, việc mã hóa các con số thập phân một cách hiệu quả và chính xác là yếu tố then chốt. Một trong những phương pháp phổ biến được sử dụng là BCD.

Định nghĩa

BCD là một loại biểu diễn nhị phân cho các giá trị thập phân, trong đó mỗi chữ số được biểu diễn bằng một số cố định các bit nhị phân, thường là từ bốn đến tám bit. Nhưng thông thường là bốn bit, biểu diễn hiệu quả các giá trị thập phân từ 0 đến 9.

Hệ thống định dạng viết này được sử dụng vì không có giới hạn về kích thước của một số. Bốn bit có thể được thêm vào như một chữ số thập phân khác, so với biểu diễn nhị phân thực, bị giới hạn ở các lũy thừa thông thường của hai, chẳng hạn như 16, 32 hoặc 64 bit.

Cấu trúc và bảng mã BCD

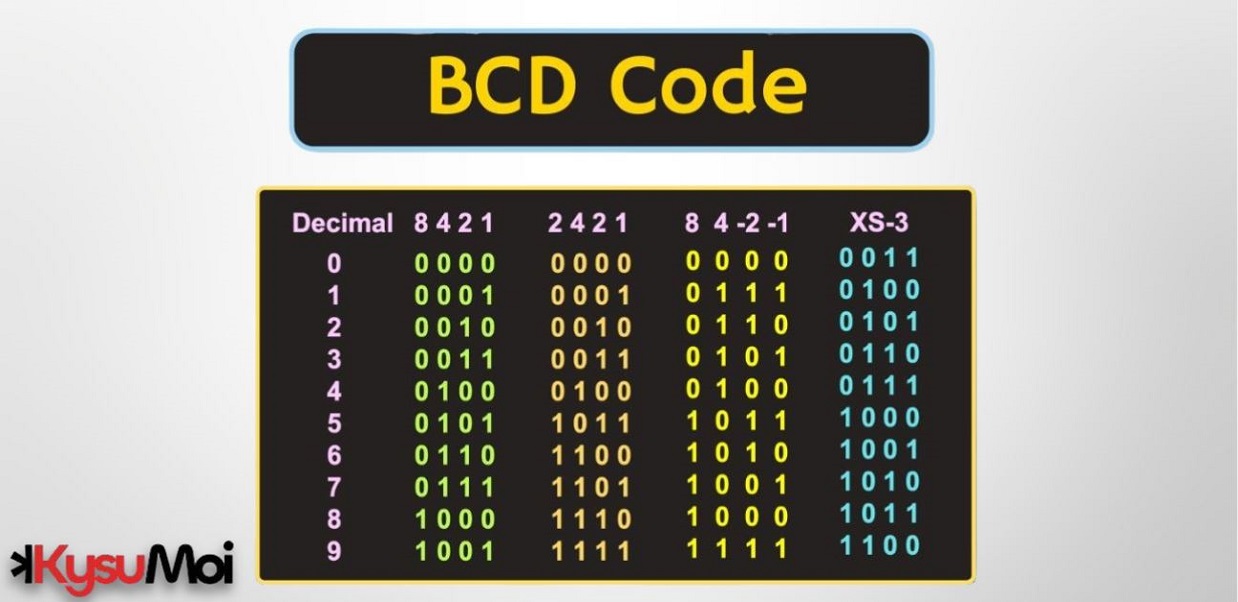
Mã BCD cấu thành từ từng nhóm 4 bit đại diện cho một chữ số thập phân (0–9). Các tổ hợp nhị phân từ 1010 đến 1111 không sử dụng; do đó, BCD không tận dụng toàn bộ không gian 4 bit, nhưng đảm bảo chuyển đổi chính xác giữa thập phân và nhị phân.

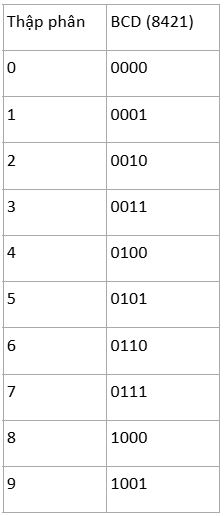
Ví dụ, số “27” trong hệ BCD được viết là “0010 0111” – mỗi 4 bit ứng với chữ số 2 và 7.

• BCD nén (packed): mỗi byte chứa 2 chữ số, tiết kiệm bộ nhớ.
• BCD không nén (unpacked): mỗi byte chứa 1 chữ số (4 bit), phần còn lại để trống hoặc dùng mục đích khác.

Cấu trúc này giúp chuyển đổi dễ dàng và chính xác trong các ứng dụng như đồng hồ số, máy tính bỏ túi, tài chính – nơi cần biểu diễn số ở dạng thập phân rõ ràng.

Toán học với BCD

1. Cộng

Khi tổng nhỏ hơn hoặc bằng 9 thì ta thực hiện phép cộng BCD như cộng nhị phân bình thường.

Ví dụ: xét phép cộng 6 và 2, dùng mã BCD biểu diễn mỗi ký số

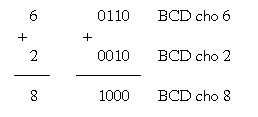
Một ví dụ khác, cộng 45 với 33

Tổng lớn hơn 9

Ta xét phép cộng 5 và 8 ở dạng BCD:

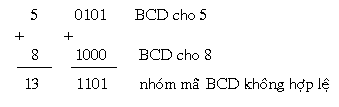
Tổng của phép cộng ở trên là 1101 không tồn tại trong mã BCD. Điều này xảy ra do tổng của hai ký số vượt quá 9. Trong trường hợp này ta phải hiệu chỉnh bằng cách cộng thêm 6 (0110) vào nhằm tính đến việc bỏ qua 6 nhóm mã không hợp lệ.

Ví dụ:

Một ví dụ khác:

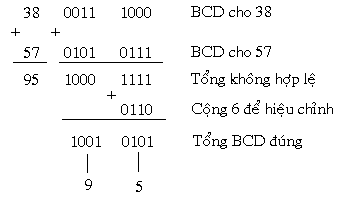
2. Trừ

Trong phép trừ nếu số bị trừ nhỏ hơn số trừ, cụ thể là khi 0 trừ 1, thì phải mượn 1 ở hàng cao kế và là 2 ở hàng đang trừ và số mượn này phải trả lại cho hàng cao kế tương tự như phép trừ của hai số thập phân.

Ví dụ 1: trường hợp trừ hai số nhị phân 1 bit

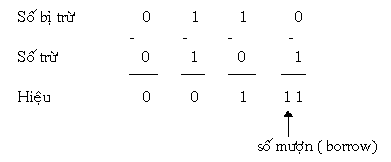
Ví dụ 2: Trừ hai số nhị phân nhiều bit

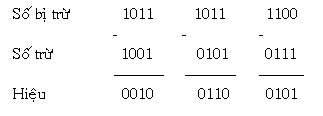
3. Nhân

Phép nhân được thực hiện tương tự như nhân số thập phân. Quá trình thật ra đơn giản hơn vì ký số của số nhân chỉ là 0 và 1, vì vậy ta chỉ nhân cho 0 hay 1.

Ví dụ:

4. Chia

Phép chia một số nhị phân (số bị chia) cho một số khác (số chia) được thực hiện giống như phép chia số thập phân. Tiến trình thựctế còn đơn giản hơn do khi kiểm tra xem có bao nhiêu lần số chia “ đi vào” số bị chia, chỉ có hai khả năng đó là 0 và 1. Quá trình chia được minh họa bằng ví dụ sau:

Trong ví dụ đầu tiên ta có 1001₂ chia cho 11₂, tương đương 9₁₀ chia cho 3₁₀

Thương số là 0011₂ = 3₁₀. Trong ví dụ thứ 2, 1010₂ chia cho 100₂ tức là 10₁₀ chia cho 4₁₀ kết quả là 0010.1₂= 2.5₁₀

Phép chia số có dấu được thực hiện như phép nhân. Số âm được biến thành số dương bằng phép bù, sau đó mới thực hiện phép chia. Nếu số bị chia và số chia có dấu ngược nhau, thương số đổi sang số âm bằng cách lấy bù 2 của nó và gán bit dấu là 1. Nếu số bị chia và số chia cùng dấu, thương số sẽ là số dương và được gán bit dấu là 0.

Ưu và nhược điểm

1. Về ưu điểm

• Quá trình chuyển đổi được đơn giản hóa: BCD giúp việc chuyển đổi giữa số nhị phân và thập phân trở nên dễ dàng hơn, đặc biệt hữu ích trong các ứng dụng máy tính và thiết bị kỹ thuật số liên quan đến xử lý số liệu thập phân như máy tính bỏ túi, đồng hồ số và các hệ thống tài chính.
• Giảm sai số trong tính toán thập phân: Vì BCD biểu diễn chính xác từng chữ số thập phân, nó giúp tránh được các sai số chuyển đổi có thể xảy ra khi sử dụng hệ thống nhị phân truyền thống, đặc biệt khi làm việc với số liệu tài chính.
• Dễ hiểu và dễ sửa lỗi: Do mỗi chữ số thập phân được mã hóa độc lập, việc xác định và sửa lỗi (nếu có) dễ dàng hơn. Ví dụ, nếu một nhóm bốn bit bị lỗi, chỉ cần sửa lại nhóm đó mà không ảnh hưởng đến toàn bộ số.

2. Về nhược điểm

• Hiệu quả bộ nhớ thấp: BCD sử dụng 4 bit để biểu diễn một chữ số thập phân (0-9). Do đó, không gian bộ nhớ không được sử dụng tối ưu vì chỉ 10 trong số 16 giá trị có thể (0000 đến 1111) thực sự được sử dụng.
• Hiệu suất tính toán thấp hơn: Các phép toán trên BCD phức tạp hơn so với các phép toán trên số nhị phân thuần túy, vì phải xử lý từng chữ số thập phân riêng lẻ và có thể cần phải điều chỉnh kết quả để đảm bảo tính hợp lệ của BCD.
• Không thích hợp cho các ứng dụng khoa học và kỹ thuật: Trong các ứng dụng khoa học và kỹ thuật, các giá trị số thường rất lớn hoặc rất nhỏ, và thường cần tính toán phức tạp. BCD không phù hợp cho các trường hợp này vì không gian bộ nhớ lớn và hiệu suất tính toán kém.

Mục đích chính

Hạn chế sai số trong hệ thống kỹ thuật số

BCD được thiết kế để giảm thiểu sai số phát sinh trong quá trình chuyển đổi giữa thập phân và nhị phân. Đây là lý do chính BCD xuất hiện trong các máy tính điện tử cũ, máy in hóa đơn hay các bộ vi xử lý có liên quan đến số liệu tài chính.

Tối ưu hóa hiển thị

Khi hiển thị dữ liệu đến người dùng, đặc biệt trên màn hình LED hoặc LCD, BCD giúp đơn giản hóa quy trình điều khiển từng chữ số thập phân. Điều này không thể thực hiện hiệu quả bằng nhị phân trực tiếp.

Dễ tích hợp vào hệ thống kế toán – tài chính

Với các hệ thống yêu cầu độ chính xác tuyệt đối trong tiền tệ, thuế hoặc hóa đơn điện tử, BCD giúp loại bỏ rủi ro sai số do làm tròn, giúp kết quả phản ánh đúng số liệu gốc.

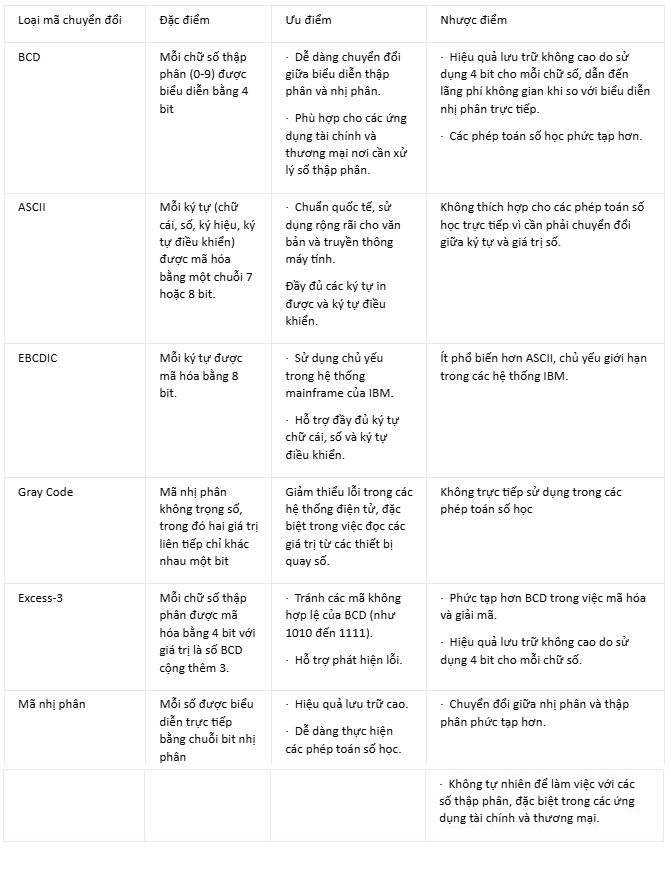
So sánh với các mã khác