Bản đồ K với các biến đã nhập

Các bản đồ biến số được nhập vào giúp đơn giản hóa quy trình hơn nữa bằng cách tối thiểu hóa trực quan bản đồ K. Việc nén bản đồ giúp hệ thống đa biến dễ hình dung và tối giản hơn nhiều.

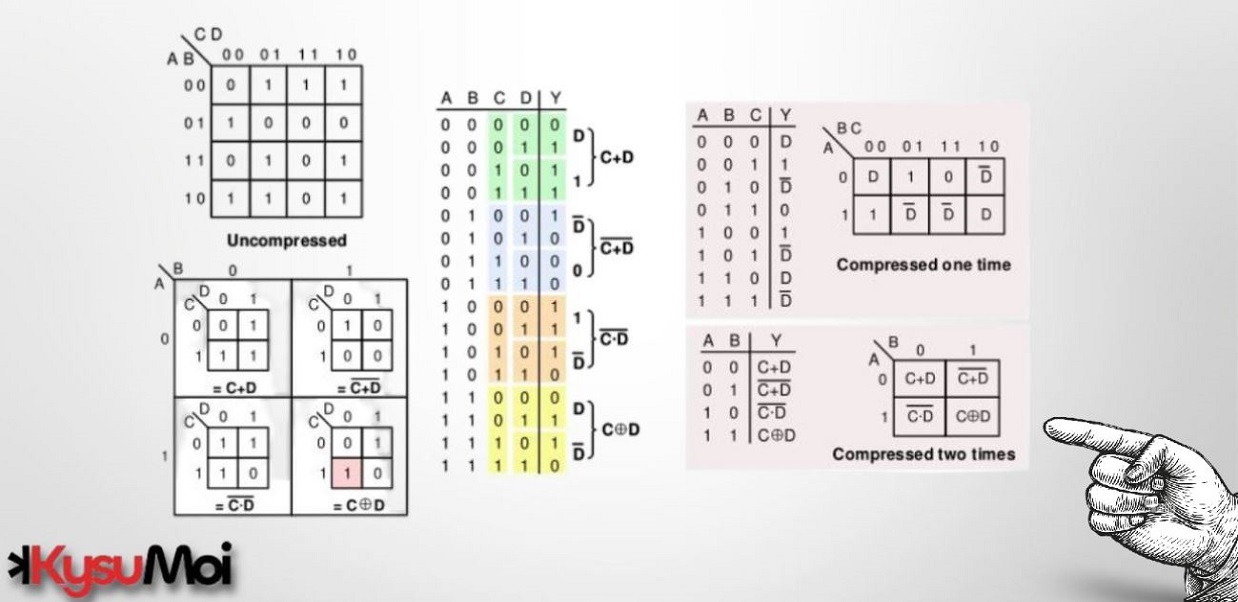
Bảng chân lý cung cấp cơ chế tốt nhất để xác định hoàn toàn hành vi của một mạch logic tổ hợp nhất định, và sơ đồ K cung cấp cơ chế tốt nhất để trực quan hóa và tối thiểu hóa các mối quan hệ đầu vào-đầu ra của mạch logic số. Cho đến nay, chúng ta đã trình bày các biến đầu vào ở phía trên bên trái của một bảng chân lý và xung quanh ngoại vi của sơ đồ K. Điều này cho phép mọi trạng thái của tín hiệu đầu ra được định nghĩa là một hàm của các mẫu đầu vào 0 và 1 trên một hàng nhất định trong bảng chân lý, hoặc là mã hóa nhị phân cho một ô sơ đồ K nhất định. Không làm mất thông tin, bảng chân lý và sơ đồ K có thể được chuyển đổi thành dạng gọn nhẹ hơn bằng cách di chuyển các biến đầu vào từ phía trên bên trái của bảng chân lý đến cột đầu ra, hoặc từ bên ngoài sơ đồ K vào bên trong các ô của sơ đồ K. Mặc dù sẽ không rõ ràng cho đến các mô-đun sau, nhưng việc sử dụng các biến đã nhập  và bảng chân lý và sơ đồ K được nén thường giúp việc trực quan hóa và tối giản hóa hệ thống đa biến dễ dàng hơn nhiều.

Cơ chế dịch chuyển được minh họa trong các hình bên dưới, trong đó một bảng chân lý 16 hàng được nén thành cả bảng chân lý 8 hàng và 4 hàng. Trong bảng chân lý 8 hàng, biến D không còn được sử dụng để xác định cột đầu vào nữa. Thay vào đó, nó xuất hiện trong cột đầu ra, nơi nó mã hóa mối quan hệ giữa hai hàng giá trị logic đầu ra và đầu vào D. Trong bảng chân lý 4 hàng, các biến C và D không còn được sử dụng để xác định cột đầu vào nữa, mà thay vào đó nằm trong cột đầu ra, nơi chúng mã hóa mối quan hệ giữa bốn hàng giá trị logic đầu ra và các đầu vào C và D.

Bản đồ K 4 ô được tái tạo ở bên phải, lần này hiển thị các bản đồ con ngụ ý minh họa mối quan hệ giữa C và D cho mỗi một trong bốn giá trị duy nhất của biến A và B. Đối với bất kỳ bản đồ K biến nào được nhập, việc suy nghĩ (hoặc thực sự phác họa) các bản đồ con có thể giúp xác định mã hóa chính xác cho các biến đã nhập. Lưu ý rằng số hàng của bảng chân lý có thể được ánh xạ vào các ô trong bản đồ con bằng cách đọc mã chỉ mục bản đồ K, bắt đầu bằng mã siêu bản đồ và thêm mã bản đồ con. Ví dụ: ô được tô bóng trong bản đồ con nằm trong ô số 1110.

Bản đồ nén này được minh họa bên dưới, cho thấy sự ánh xạ trực tiếp từ bản đồ K không nén sang bản đồ K nén. Màu sắc thể hiện cách các ô trong bản đồ không nén được dịch chuyển sang các ô trong bản đồ nén. Lưu ý rằng hai ô trong bản đồ 16 ô được nén thành một ô duy nhất trong bản đồ 8 ô, và bốn ô trong bản đồ 16 ô được nén thành một ô duy nhất trong bản đồ 4 ô.

Phương trình SOP Minterm và phương trình POS Maxterm cũng có thể được dịch trực tiếp sang các bản đồ K-map biến đã nhập như minh họa bên dưới (các số nhỏ hơn ở cuối ô bản đồ K-map hiển thị số minterm hoặc maxterm được gán cho ô đó). Số lượng biến đầu vào tối thiểu được giả định khi mã hóa minterm hoặc maxterm vào bản đồ K-map. Ví dụ: nếu minterm lớn nhất hiện có là 14, bốn biến đầu vào sẽ được giả định.

Việc lặp các bản đồ K biến nhập vào tuân theo các nguyên tắc chung giống như lặp các bản đồ '1-0'—tìm kiếm các nhóm tối ưu của các số 1 và các biến nhập vào (EV) cho các mạch SOP, và tìm kiếm các nhóm tối ưu của các số 0 và EV cho các mạch POS. Các quy tắc tương tự nhau: tất cả các EV và tất cả các số 1 (hoặc 0) phải được nhóm thành nhóm hình chữ nhật hoặc hình vuông có kích thước "lũy thừa của 2" lớn nhất có thể, và quá trình hoàn tất khi tất cả các EV và tất cả các số 1 (hoặc 0) được đưa vào một vòng lặp tối ưu. Sự khác biệt là các EV tương tự có thể được bao gồm trong các vòng lặp riêng lẻ hoặc với 1 (hoặc 0), và phải cẩn thận khi lặp các ô với 1 (hoặc 0), vì '1' (hoặc '0') chỉ ra rằng tất cả các tổ hợp EV có thể có đều có trong ô bản đồ đó và các vòng lặp bao gồm 1 (hoặc 0) cùng với EV thường chỉ bao gồm một tập hợp con các tổ hợp EV có thể có (điều này được minh họa trong Hình 4 bên dưới). Lặp một bản đồ K EV hoàn tất khi tất cả các minterm hoặc maxterm được chứa trong một nhóm thích hợp. Có lẽ khía cạnh thách thức nhất là đảm bảo rằng tất cả các tổ hợp EV có thể có đã được tính đến trong các ô chứa 1 (hoặc 0).

Để hiểu rõ hơn về vòng lặp trong EV K-map, việc xem xét các bản đồ con được ngụ ý bởi mỗi ô K-map có thể hữu ích. Như được minh họa trong các hình bên dưới, các biến trong các ô K-map có thể phát sinh từ việc lặp thông tin '1-0' được nhập vào các ô trong các bản đồ con ngụ ý. Một vòng lặp thông tin trong các ô liền kề trong EV K-map có thể bao gồm các số 1 (hoặc 0) trong các bản đồ con xuất hiện ở cùng vị trí trong các bản đồ con.

Khi đọc các phương trình vòng lặp, các số hạng tích SOP (hoặc tổng POS) của mỗi vòng lặp phải bao gồm các biến xác định miền lặp và các EV chứa trong vòng lặp. Ví dụ, trong ví dụ đầu tiên bên dưới, số hạng SOP đầu tiên A.B.D. bao gồm miền vòng lặp A.B và biến D được nhập vào.

Các ô trong bản đồ biến đã nhập có thể chứa một biến đã nhập duy nhất hoặc một biểu thức logic của hai hoặc nhiều biến. Khi lặp các ô chứa biểu thức logic, việc nhận ra sự khác biệt trong cơ chế lặp SOP và POS sẽ hữu ích. So với một EV đơn lẻ trong ô bản đồ K, một tích số trong ô biểu diễn một miền SOP nhỏ hơn, vì càng nhiều biến AND trong một tích số thì miền logic được xác định càng nhỏ. Một tổng số trong ô biểu diễn một miền SOP lớn hơn, vì càng nhiều biến OR trong một tổng số thì miền logic được xác định càng lớn. Khi lặp các phương trình SOP từ bản đồ EV, các ô chứa tích số có ít số 1 trong bản đồ con của chúng hơn các ô chứa EV đơn lẻ và các ô có tổng số chứa nhiều số 1 hơn. Tương tự, khi lặp các phương trình POS từ bản đồ EV, các ô chứa tổng số có ít số 0 hơn trong bản đồ con của chúng so với các ô chứa EV đơn lẻ và các ô có tích số chứa nhiều số 0 hơn.

Các phép toán Don't care trong biến đã nhập K-map có cùng mục đích như trong các phép toán '1-0'; chúng biểu thị các điều kiện đầu vào không thể xảy ra hoặc không liên quan, và chúng có thể được đưa vào các nhóm 1, 0 hoặc biến đã nhập tùy theo nhu cầu để tối giản logic. Như minh họa trong Hình 5 bên dưới, một phép toán Don't care cho trước có thể được coi là biến '1', '0' hoặc biến đã nhập tùy theo nhu cầu cho bất kỳ vòng lặp cụ thể nào.

‍

Ý tưởng quan trọng

• Không làm mất thông tin, bảng chân lý và bản đồ K có thể được chuyển đổi thành dạng gọn hơn bằng cách di chuyển các biến đầu vào từ góc trên bên trái của bảng chân lý đến cột đầu ra hoặc từ bên ngoài bản đồ K vào bên trong các ô của bản đồ K.
• Các phương trình SOP minterm và các phương trình POS maxterm cũng có thể được dịch trực tiếp thành các bản đồ K biến đã nhập.
• Lặp các biến K-map đã nhập tuân theo các nguyên tắc chung giống như lặp các bản đồ '1-0'.
• Các ô trong bản đồ biến đã nhập có thể chứa một biến đã nhập hoặc một biểu thức logic của hai hoặc nhiều biến.
• Không quan tâm đến biến đã nhập, bản đồ K có cùng mục đích như trong bản đồ '1-0'.