Phương pháp Quine McCluskey, còn được gọi là phương pháp lập bảng , là một phương pháp rất hữu ích và tiện lợi để đơn giản hóa các hàm Boolean cho một số lượng lớn biến (lớn hơn 4). Phương pháp này hữu ích hơn so với bản đồ K khi số lượng biến lớn hơn mà việc lập bản đồ K gặp khó khăn. Phương pháp này đơn giản hóa các hàm bằng cách xác định và lựa chọn các hàm nguyên tố một cách có hệ thống.

Trong phương pháp này, chúng tôi xây dựng nhiều bảng dựa trên hàm đầu vào và cuối cùng, tạo một bảng hàm nguyên tố, được sử dụng để thu được các hàm nguyên tố thiết yếu có trong biểu thức Boolean đã được đơn giản hóa. Phương pháp này yêu cầu kiến ​​thức nền tảng về biểu diễn thập phân sang nhị phân và các kiến ​​thức cơ bản về đại số Boolean. Đây là một phương pháp phù hợp với số lượng lớn các biến đầu vào có thể dễ dàng giải bằng phương pháp này, nhưng độ phức tạp tính toán lại cao. Về cơ bản, phương pháp này bao gồm việc sử dụng các minterm và các hàm nguyên tố thiết yếu, từ đó thu được các hàm nguyên tố thiết yếu, sau đó được sử dụng trong các hàm Boolean đã được đơn giản hóa. 

Thuật ngữ

• Hàm ẩn: Hàm ẩn được định nghĩa là một nhóm gồm 1 (đối với minterm).  
• Hàm ý chính: Đây là nhóm 1 lớn nhất có thể (đối với minterm).
• Nhóm hàm ý chính thiết yếu: Đây là những nhóm bao gồm ít nhất một minterm mà các nhóm hàm ý khác không thể bao gồm.

Lưu ý: Phương pháp này yêu cầu chuyển đổi các minterm thập phân sang dạng biểu diễn nhị phân để nhóm.

Các bước thực hiện phương pháp Quine McCluskey

1. Sắp xếp các minterm đã cho theo số lượng đơn vị có trong biểu diễn nhị phân của chúng theo thứ tự tăng dần.
2. Lấy các minterm từ nhóm liên tục nếu chỉ có một thay đổi bit để tạo thành cặp của chúng. 
3. Đặt ký hiệu '-' vào nơi có sự thay đổi bit tương ứng và giữ nguyên các bit còn lại.
4. Lặp lại các bước từ 2 đến 3 cho đến khi chúng ta có được tất cả các phần tử nguyên tố (khi tất cả các bit có trong bảng đều khác nhau).
5. Tạo một bảng hàm ý nguyên tố bao gồm các hàm ý nguyên tố (minterm thu được) dưới dạng hàng và các minterm đã cho (có trong bài toán) dưới dạng cột.
6. Đặt '1' vào các ô tương ứng với các minterm được bao phủ bởi mỗi hàm ý chính
7. Hãy quan sát bảng, nếu một minterm chỉ được bao phủ bởi một hàm ý chính thì nó là yếu tố cần thiết đối với hàm ý chính đó.
8. Thêm các hàm ý nguyên tố thiết yếu vào hàm Boolean đã được đơn giản hóa. 

Các ví dụ đã giải của phương pháp Quine McCluskey

Ví dụ: Rút gọn bằng phương pháp lập bảng: F(A,B,C,D) =∑ m(0,1,2,4,6,8,9,11,13,15)

Giải pháp: Chuyển đổi các minterm đã cho thành dạng biểu diễn nhị phân của chúng và sắp xếp chúng theo số lượng đơn vị có trong dạng biểu diễn nhị phân. 

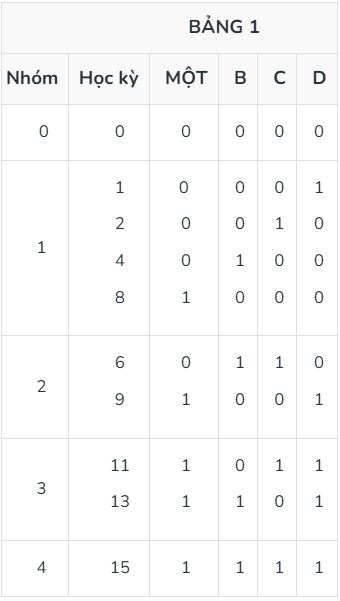
Vì 0 không có số 1 trong biểu diễn của nó nên nó được giữ trong một nhóm (0). Tương tự, 1 2 4 và 8 chứa một số 1 trong biểu diễn của chúng nên nó được giữ trong nhóm tiếp theo (1). 6 và 9 trong nhóm tiếp theo (2), 11 và 13 trong nhóm tiếp theo (3), 15 trong nhóm cuối cùng (4). 

Bây giờ, đối với bảng 2, hãy lấy các minterm từ các nhóm liên tiếp (chỉ nhóm đồng thời) có sự khác biệt chỉ 1 bit trong biểu diễn của chúng và tạo thành cặp của chúng bằng cách hợp nhất chúng và tạo thành một nhóm các cặp đến từ cùng một nhóm được hợp nhất (ví dụ 0 đến từ nhóm 0 và 1 đến từ nhóm 1 nên nó được thêm vào nhóm 0. 0 thuộc nhóm 0 trong bảng 1 và 2 thuộc nhóm 1 trong bảng 1 nên nó được giữ trong cùng một nhóm trong bảng 2. Tương tự, hãy tạo tất cả các cặp có thể với sự trợ giúp của bảng trên và đánh dấu - nơi có sự khác biệt bit. 

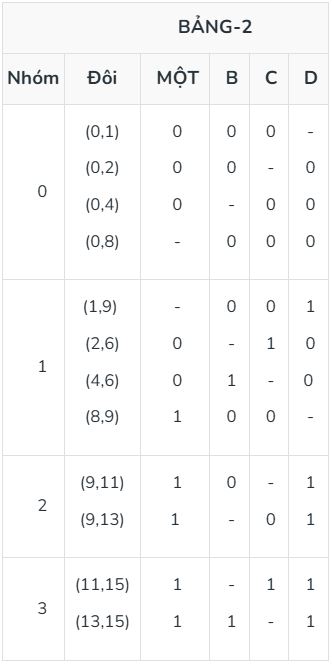
Đối với bảng 3, hãy lặp lại bước tương tự bằng cách lấy các cặp nhóm liên tiếp, hợp nhất chúng ở những nơi chỉ có sự khác biệt 1 bit và giữ chúng trong các nhóm theo nhóm mà chúng được hợp nhất và đặt vào - theo sự khác biệt bit.

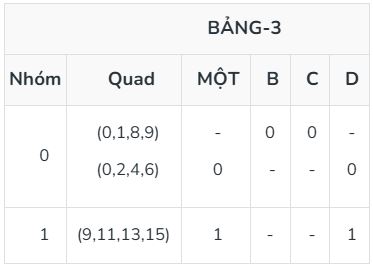
Sau bảng 3, quá trình dừng lại vì không có sự khác biệt 1 bit nào trong các minterm nhóm còn lại trong các nhóm đồng thời của bảng 3.

Bây giờ, các phần tử tứ phân còn lại trong bảng 3 biểu diễn các hàm nguyên tố cho hàm Boolean đã cho. Vì vậy, chúng ta xây dựng bảng hàm nguyên tố, chứa các hàm nguyên tố thu được dưới dạng hàng và các minterm đã cho dưới dạng cột. Đặt 1 vào vị trí tương ứng mà minterm có thể biểu diễn. Thêm minterm vào biểu thức Boolean đã được rút gọn nếu minterm đã cho chỉ được bao phủ bởi hàm nguyên tố này.  

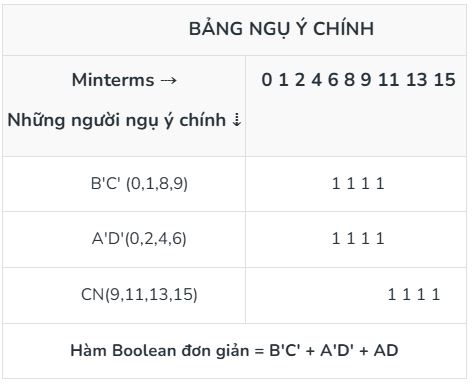
B'C' ở dạng hàm đơn giản vì minterm 1 chỉ được bao phủ bởi B'C'. Tương tự, minterm 2, 4, 6 chỉ được bao phủ bởi A'D' và minterm 11, 13, 15 chỉ được bao phủ bởi AD.

Ví dụ: Rút gọn bằng phương pháp lập bảng: F(A,B,C,D,E,F,G) = ∑m(20,28,52,60)

Giải pháp: Chuyển đổi các minterm đã cho thành dạng biểu diễn nhị phân và sắp xếp chúng theo số lượng đơn vị có trong dạng biểu diễn nhị phân. 

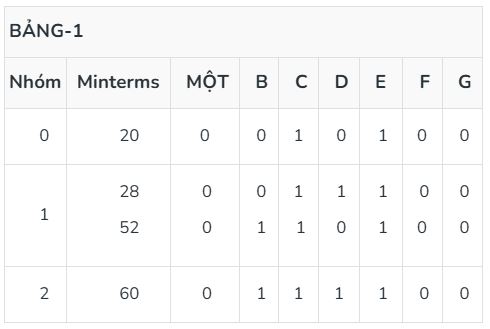
Vì 20 có 2 số 1 trong biểu diễn của nó nên nó được giữ trong một nhóm (0). Tương tự, 28 và 52 chứa 3 số 1 trong biểu diễn của chúng nên nó được giữ trong nhóm tiếp theo (1). 60 trong nhóm tiếp theo (2).

Bây giờ, đối với bảng 2, hãy lấy các minterm từ các nhóm liên tiếp (chỉ nhóm đồng thời) có sự khác biệt chỉ 1 bit trong biểu diễn của chúng và tạo thành cặp của chúng bằng cách hợp nhất chúng và tạo thành một nhóm các cặp đến từ cùng một nhóm được hợp nhất (ví dụ 20 đến từ nhóm 0 và 28 đến từ nhóm 1 nên nó được thêm vào nhóm 0. 20 thuộc nhóm 0 trong bảng 1 và 52 thuộc nhóm 1 trong bảng 1 nên nó được giữ trong cùng một nhóm trong bảng 2. Tương tự, hãy tạo tất cả các cặp có thể với sự trợ giúp của bảng trên và đánh dấu - nơi có một chút khác biệt. 

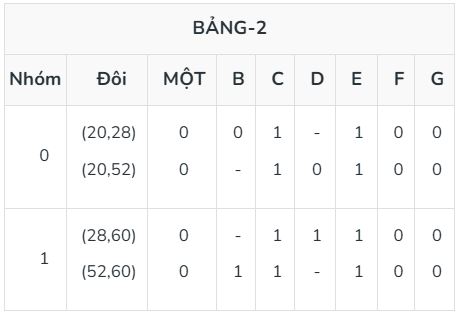
Đối với bảng 3, hãy lặp lại bước tương tự bằng cách lấy các cặp nhóm liên tiếp, hợp nhất chúng ở những nơi chỉ có sự khác biệt 1 bit và giữ chúng trong các nhóm theo nhóm mà chúng được hợp nhất và đặt vào - theo sự khác biệt bit.

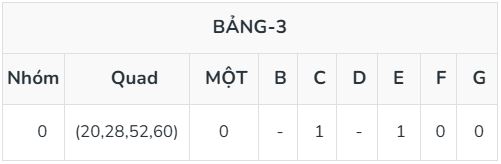
Sau bảng 3, quá trình dừng lại vì không có sự khác biệt 1 bit nào trong các minterm nhóm còn lại trong các nhóm đồng thời của bảng 3.

Bây giờ, các phần tử tứ phân còn lại trong bảng 3 biểu diễn các hàm nguyên tố cho hàm Boolean đã cho. Vì vậy, chúng ta xây dựng bảng hàm nguyên tố, chứa các hàm nguyên tố thu được dưới dạng hàng và các minterm đã cho dưới dạng cột. Đặt 1 vào vị trí tương ứng mà minterm có thể biểu diễn. Thêm minterm vào biểu thức Boolean đã được rút gọn nếu minterm đã cho chỉ được bao phủ bởi hàm nguyên tố này. 

A'CEF'G' được lấy từ bảng 3 vì A, F, G chứa 0 nên A'F'G', C và E chứa 1 nên CE. 

A'CEF'G' có chức năng đơn giản hóa vì nó là hàm ý nguyên tố duy nhất bao hàm tất cả các minterm.

Ưu điểm của phương pháp Quine McCluskey

• Phương pháp này phù hợp với số lượng lớn đầu vào (n>4) mà việc xây dựng bản đồ K là một nhiệm vụ tẻ nhạt.
• Nó không yêu cầu phải nhận dạng mẫu.
• Nó cung cấp một phương pháp tiếp cận có hệ thống và theo bảng.
• Đảm bảo dạng Tổng các sản phẩm (SOP) hoặc Tích các tổng (POS) tối thiểu.

Nhược điểm của phương pháp Quine McCluskey

• Độ phức tạp tính toán của phương pháp này rất cao.
• Việc này trở nên không thực tế đối với các hàm có nhiều hơn 6-7 biến do bảng lớn.
• Phương pháp này ít trực quan hơn và khó sử dụng thủ công hơn so với Bản đồ Karnaugh cho các hàm nhỏ hơn